Roux — Last Six Edges
Contents
- Overview
- Novice LSEa
- Novice LSEb
- Novice LSEc
- Intermediate Efficiency
- Intermediate DFDB
- Advanced EOLR
Overview
In LSE we will solve the last six edges (all four U layer edges and the DF and DB edges) of the cube intuitively using only M slice moves and U face turns and the occasional E2 move. The genius and simplicity of this step are what the Roux method is known for. Arbitrary M and U moves don't disturb the top layer corners relative to each other nor do they disturb our first two blocks at all, and so amazingly M and U are both powerful enough to solve the rest of the cube and restricted enough to do no damage. This makes LSE extremely efficient. There is a slight further efficiency boost we can get from also using E2 moves though they aren't strictly necessary. An E2 does break first two blocks, but it does it so mildly that as long as we do another E2 later it doesn't matter what M or U turns are inbetween, the first two blocks will be restored.
We approach LSE in three substeps, LSEa, LSEb, and LSEc. In LSEa we orient all 6 edges. In LSEb we solve the UL and UR edges simultaneously, leaving only the edges on the M slice. In LSEc we solve all the M slice edges simultaneously. More advanced Rouxers are able to partly or entirely combine LSEa and LSEb so that they orient the 6 edges while solving UL and UR. Intermediate to advanced Rouxers are also able to smoothly predict and influence what LSEc cases they will get while doing LSEb. These advancements make the three substeps of LSE flow smoothly and efficiently without pauses.
Coming out of CMLL, the U layer can be aligned in any of 4 permutations and the M slice can be aligned in any of 4 independent permutations. The UB edge can be in any of 6 permutations with 2 possible orientations. Further, UR has 5 perms and 2 ors, UF has 4 perms and 2 ors, UL has 3 perms and 2 ors. The permutations of DF and DB are fixed given all of that previous data. DF still has two possible ors, which then fixes the orientation of DB. Thus, for LSE there are in principle 184320 cases. This is a much smaller number than either first or second block and so it was simple to write code to solve them optimally. Below you will find the distribution of optimal solution lengths. I also wrote an explicit optimal LSE solver that you can use. Note that these solutions are optimal among those making use of only M U and E2 moves.
Last Six Edges Statistics
| Average Moves: | 11.13 |
| Standard Deviation: | 1.84 |
| Median Moves: | 11 |
| 95th Percentile: | 14 |
| Max Moves: | 20 |
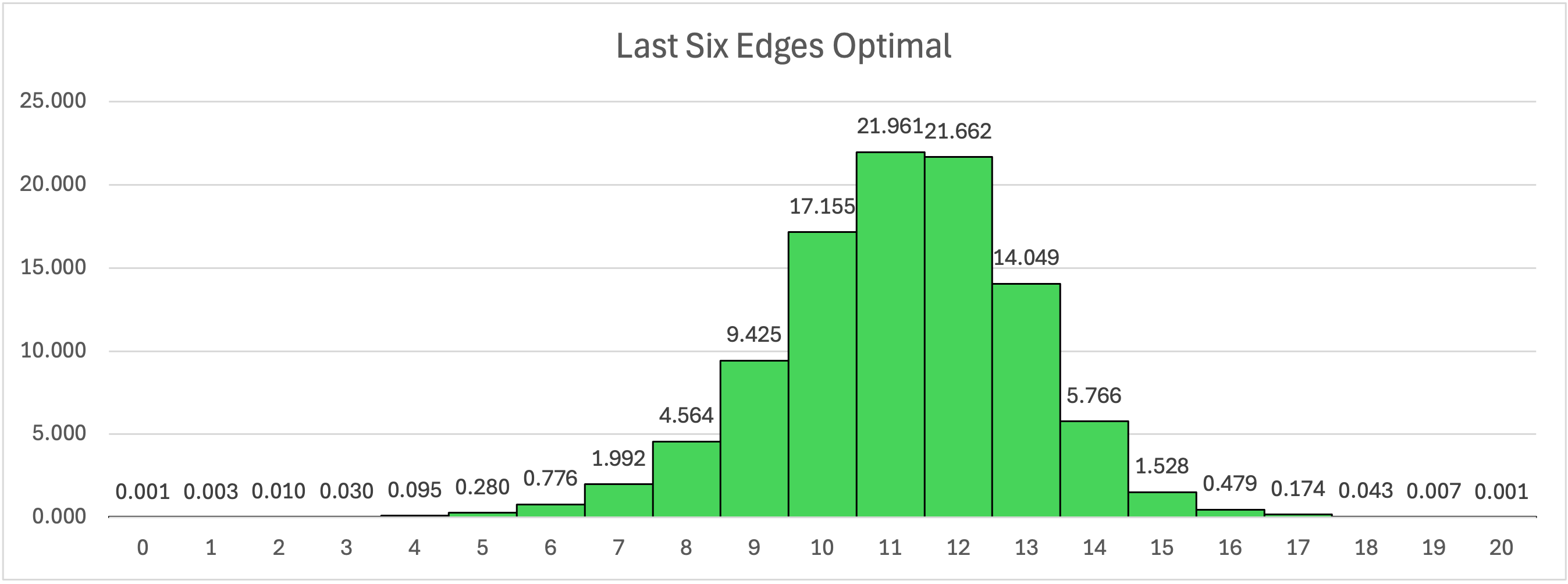
There are only 2 LSE states that require 20 moves to solve. One of the 20 move states is the scramble M' U' M' U' M' U' M2 U' M U2 M' U M' U M U2 M U M U and the other is its inverse U' M' U' M' U2 M' U' M U' M U2 M' U M2 U M U M U M.
Novice LSEa
We start LSE by orienting the last six edges. To begin, align your M slice so that the center on the U face is either the top color or bottom color. For example, if you are solving Blue on top, then align the M slice so that either the Blue or Green center is on top. All of the last six edges have one sticker that is the top or bottom color (Blue or Green) and one sticker that isn't. An edge is good
, meaning properly oriented, if its top/bottom color is actually on the top or bottom (a Green sticker on the Blue or Green face is good, a Blue sticker on the Blue or Green face is good, any side color on the Blue or Green face is bad). By aligning the U layer appropriately, there are 12 possible edge orientation cases. We move case to case following a little flow chart until we reach all edges being oriented correctly. Whenever you do an M slice move, it flips all 4 edges on the M slice. So, a single M or M' followed by a U or U' followed by an M or M' will keep the top center as either the top or bottom color and flip some edges. This makes M' U M' the basic mini-alg that takes us between our different cases.
Below are the 12 cases and their names (with the top and bottom view), followed by the flow chart for how we move between them. You shouldn't be trying to memorize these explicitly, rather you should learn how they connect intuitively. Because there are so few cases you will quickly internalize the flow chart. The Cyan color is allowed to be either Blue or Green, because for this step they count as the same.
You might be worried that for this step you have to somehow look at the top and bottom of the cube at the same time, but you don't! By holding the cube so that you can see the U face the F face as usual, you can tell whether the top layer edges are oriented directly and whether the Down-Front edge is oriented by whether you see a side color on the F face (good) or a top/bottom color on the F face (bad). You can then infer whether the Down-Back edge is oriented because the total number of good edges is always even. Basically, you should learn what these 12 cases look like from the U F perspective because the DB edge that you can't see is always implied by what you can see from those two faces. The D face shown in the images below is so that the faces are exactly aligned with the U face, meaning for example that in the 1 + 1 Front case, the misoriented edge is in the DF position (look at the picture to see what I mean).
There are some common nicknames for the different edge orientation cases given in the chart below. There is also a systematic naming scheme of the format XA/YB where X is the number of bad edges in U layer, A is absent unless X is 2 in which case A is either o (meaning the two U layer bad edges are opposite each other) or a (meaning the two U layer bad edges are adjacent to each other), Y is the number of bad edges in the D layer, and B is absent unless Y is 1 in which case B is either f (meaning the bad edge is in the DF spot) or b (meaning the bad edge is in the DB spot).
| Solved! 0/0 |
D-Line 0/2 |
||||
| 1 + 1 Front 1/1f |
1 + 1 Back 1/1b |
||||
| V 2a/0 |
V + D-Line 2a/2 |
||||
| U-Line 2o/0 |
(U + D)-Line 2o/2 |
||||
| F Arrow 3/1f |
B Arrow 3/1b |
||||
| Cross 4/0 |
6 Flip 4/2 |
Novice LSEb
Fortunately, LSEa is the hardest part of LSE, and you got through it! LSEb is the easiest part. Now that we have solved edge orientation, we never should alternate single turns of the M slice with single turns of the U face, as that would mess up our orientation. So, now if we do a single U or U' we have to follow it with an M2 and if we do a single M or M' we have to follow it with a U2. With these combinations edge orientation will be preserved.
In this substep we are going to solve the UL and UR edges simultaneously. We do this in three little microsteps. First, we put one of the Ul/UR edges in the bottom layer using an M2 and align the U layer so that the other UL/UR edge is completely diagonally opposite of the other one. That means we either (1) put one edge in the DF position and the other in the UB position or (2) put one edge in the DB position and the other in the UF postion. Second, in case (1) we do M' U2 M' or in case (2) we do M' U2 M. This puts both the UL and UR edges in the D layer in a line with each other. Finally, we align the top layer so that the corner stickers on the F face are the opposite color of sticker shown on the F face by the edge in the DF position. From here, an M2 solves both the UL and UR edges simultaneously! We then finally adjust the U layer so that all of the corners are back where they belong. That description might be too abstract, so let's do an example.
| Let's assume coming our of LSEa we are in a state like this. Blue-White and Blue-Yellow are our UL/UR edges. If we do an M2 from here Blue-White will go to the DB position. Then, a U brings Blue-Yellow to the diagonal UF position. | Blue-White and Blue-Yellow are positioned in DB and UF so we are in case (2). This means we do M' U2 M. | ||
| Blue-White and Blue-Yellow are now positioned in DB and DF. Because Blue-Yellow is in the DF spot, we turn the U layer until the White corner stickers are on the F face. Here this means we do a U'. | From here a simple M2 will place both Blue-White and Blue-Yellow! | ||
| Now we just turn the U layer until the corners are aligned properly. Here this means we need a U. | Now the entire cube except for the M slice should be solved! |
Novice LSEc
After LSEb, by moving just the M slice you will land in one of 5 cases. One of them is a solved cube (congrats, you got a little lucky). The other 4 aren't quite as easy but they still aren't too hard! In order to not mess up what we have done so far, we can still use M moves however we like but can now only do U2 moves. For this substep, the case only depends on the relative colors of the M slice, not the absolute colors. By this I mean I will show the 4 cases with 4 pictures but in each of those 4 pictures you could color-swap Blue with Green and Red with Orange OR Blue with Red and Green with Orange OR Blue with Orange and Green with Red. No matter which of those swaps you do, you still have the same case. For this step you might have to move the M slice around a bit to figure out which case you are in.
| Clockwise 3-Cycle (viewed from the right side). Here UB, UF, and DF are unsolved. U2 M' U2 M |
Counterclockwise 3-Cycle. Here UB, UF, and DF are unsolved. M' U2 M U2 |
||
| H M2 U2 M2 U2 |
Dots M' E2 M E2 |
After applying whatever the appropriate case is, you might still have to align the M slice to finish the cube. Doing so should bring you to the end of your first Roux solve!
Intermediate Efficiency
Generally at intermediate level the overall strategy of LSE doesn't change at all. However, you can optimize the Novice approach by more smoothly canceling moves between the different substeps. They should flow together better at intermediate level. To start, at intermediate level you should always be orienting your edges in the optimal number of moves. A novice might view 1+1 F and 1+1 B as different cases, but you should now think of them as the same (just mirrors of each other, and so having mirror solutions). Similarly, F arrow and B arrow are mirrors. A novice will always set up a V case so that the unoriented edges are in UB and UL positions, but an intermediate solver knows how to optimally orient a V no matter how the U face is aligned (again just some mirroring). So, past the novice level the systematic edge orientation labelling is just XA/Y, because the previous B label can be excluded by mirroring. Below are some move optimal edge orientation algorithms for each of the 9 nonsolved orientation cases (mirrors excluded). But, many of these cases have many optimal solutions, so just make sure you are using ones that are easy in your hands and of equal lengths to these.
| D-Line (0/2) | M' U M' U' M U M | 1+1 B (1/1) | M' U' M' U2 M U M' | V (2a/0) | M' U M' U2 M' U M' |
| V + D-Line (2a/2) | M2 U' M' U M' | U-Line (2o/0) | M' U M' U' M' U M' | (U+D)-Line (2o/2) | M' U2 M' U2 M U M |
| F Arrow (3/1) | M' U M' | Cross (4/0) | M' U2 M' U2 M' U M' | 6 Flip (4/2) | M' U M' U M U M U2 M' U M' |
At the intermediate level, while you are doing LSEa you should be watching the locations of your UL/UR edges so that you can flow seemlessly into LSEb. Often the last move or two of LSEa can be canceled by the first move or two of LSEb, reducing your overall movecount. Because there are many optimal ways to do EO (edge orientation), you can even cleverly pick one which makes LSEb more efficient. This kind of thinking is made more exact at the advanced level, but you can still partly do it here. Cancelations can also happen going from LSEb into LSEc. At the intermediate level you should rarely be doing the full 4-move novice LSEc algorithms
. Instead, most of the time you are going to setup coming out of LSEb so that only the last 3 (and sometimes even just the last 2) moves of those algs are necessary. You can practice these cancelations by just doing some practice solves where you do LSE really slowly and try to focus on efficiency.
Intermediate DFDB
LSEc recognition the novice way sucks. Having to move the M slice around until you figure out what case you are in is slow and inefficient. At the intermediate level, you should learn to predict the LSEc case you are going to have while you are doing LSEb. This will make your solve so much smoother. The scheme by which we do this is called DFDB, because you will be inferring what will be going on with those edges during LSEc by stuff you can see in LSEb. The basic problem with LSEc is that just looking at the U and F faces of the cube after doing LSEb, you can't always unambiguously tell what case you have. You can tell what case you have if the case is an H or Dots case. But, if it is one of the 3-cycle cases it is ambiguous. By doing a little tracking of other pieces in LSEb, we can resolve this ambiguity.
Let's say you have done LSEb up to the point that the UL/UR edges are in the D layer and the U layer is aligned so that if you do an M2 then they will be properly inserted. Since we are now doing the DFDB method, instead of just finishing up LSEb, at this moment we look at the edge in the UF position. If it is a top layer edge, then there will be one other top layer edge actually in the top layer. That is called its friend edge. It if is a bottom layer edge, then there will be one other bottom layer edge actually in the top layer. Then that is called its friend edge. If the friend edges are opposite to each other (meaning in the UF and UB positions), then you will have a non-cycle LSEc (meaning you will get either H or Dots). In the non-cycle case, just do the M2 insert to finish LSEb and go onto LSEc and do your H or Dots, because it will be unambiguous
The interesting part of DFDB is when the friend edges are next to each other (meaning one of them is in the UF position and the other is in either the UR or UL position). This will be a cycle case for LSEc. Now we need to check something else. Look at the F face. Either the center piece color will match the F face sticker of the UF edge or they will be opposite colors. These two cases are called Matching Center and Non-Matching Center. Once you know whether you have the Matching Center or Non-Matching Center case, you should M2 to finish LSEb.
Let's first discuss the Matching Center case. After you have M2'd to finish LSEb, in the Matching Center case you now align the U layer so that the friend edge which is still in the top layer is moved to the UF position. If the friend edge was at UR in LSEb, this means you need to do U and if it was at UL, you need to do a U'. Once you have put the friend edge at UF, we do what is calling raising the dots
. On the U face at this point, one of the edge stickers will match the center and one of them will be colored oppositely to the center. The oppositely colored edge sticker we call a dot. To raise a dot, you do either an M or an M', whichever one moves the dot across the U face, followed by a U2. If the dot is at UB, you do M U2. If the dot is at UF, you do M' U2. After raising the dot, there may be a new dot on the U face. If there is, then raise the dot again. Once there is no dot on the U face, aligning the M slice will solve the cube.
Now let's discuss the Non-Matching Center case. In this case, after you have M2'd to finish LSEb, you now align the U layer so that the corners are properly aligned. Then, you note where the remaining top layer friend edge is. It will either be in UF or UB. If it is in UF, simple raise the dots, just like in the Matching Center case. If it is in UB, do M2 U2 then raise the dots. Align the M slice will finish the cube. That was a lot to describe, so I've made a flowchart and we will do some examples.
| You have Blue-White and Blue-Yellow to be M2'd. Because Green-Red is at UF, we look for the friend edge Green-Orange, which here is at UR. So, we are in a cycle case. The Red of Green-Red matches the Red center on the F face, giving Matching Center case. So, do an M2 to finish LSEb then a U to put the friend edge at UF. | Now we raise dots. The dot is at UB so we do M U2. | ||
| We have no more dot on the U face, so we just adjust the M slice to finish. | Done! |
| Another example. Blue-Orange is at UF, so we look for the other Blue edge, which here is at UL (another cycle!). The Orange of Blue-Orange does not match the Red center on the F face, giving Non-Matching Center case. So, do an M2 to finish LSEb then a U to solve the corners. | The friend edge moved from UL to UB when we did a U. So, we next need to do M2 U2. | ||
| Now we can raise dots. The dot is at UF so we do M' U2. | I think you can handle it from here. |
Advanced EOLR
At the advanced level of Roux solving, we basically combine LSEa and LSEb into one substep called EOLR (Edge Orientation, which is LSEa, and Left Right for solving UL and UR, which is LSEb). The goal of EOLR is to orient all the edges so that when we end edge orientation, the UL and UR edges are both in the D layer. By having them in the D layer, we are then perfectly set up for using DFDB to finish up the cube. Like the rest of LSE, EOLR is still intuitive in the sense that you shouldn't try to explicitly enumerate and memorize all the cases. Instead, you should study the cases by watching how they move pieces around until you get a feel for how to do it in a real solve.
I haven't actually finished learning EOLR, so I don't think I am qualified yet to write this section. Instead, I'll refer you to Kian Mansour's EOLR guide and this helpful series of short videos on how EOLR works.