Roux — CMLL
Contents
Overview
In CMLL we will solve the four corners of the U face using an algorithm. We do this without caring at all about the alignment of the M slice. When you are a novice, you will do this in 2 steps. First (neglecting solved cases) you orient the corners in one of seven cases and second you permute the corners in one of two cases, thus requiring 9 total algorithms. When you are intermediate, you will learn to do it in 1 step, which then has 42 cases. When you are advanced, you will learn how to recognize those 42 cases from any angle so that you never have to waste moves adjusting the U face to figure out which case you have. The algorithms for CMLL are very ergonomic and nice. It is a very useful and simple set to learn, so don't be afraid.
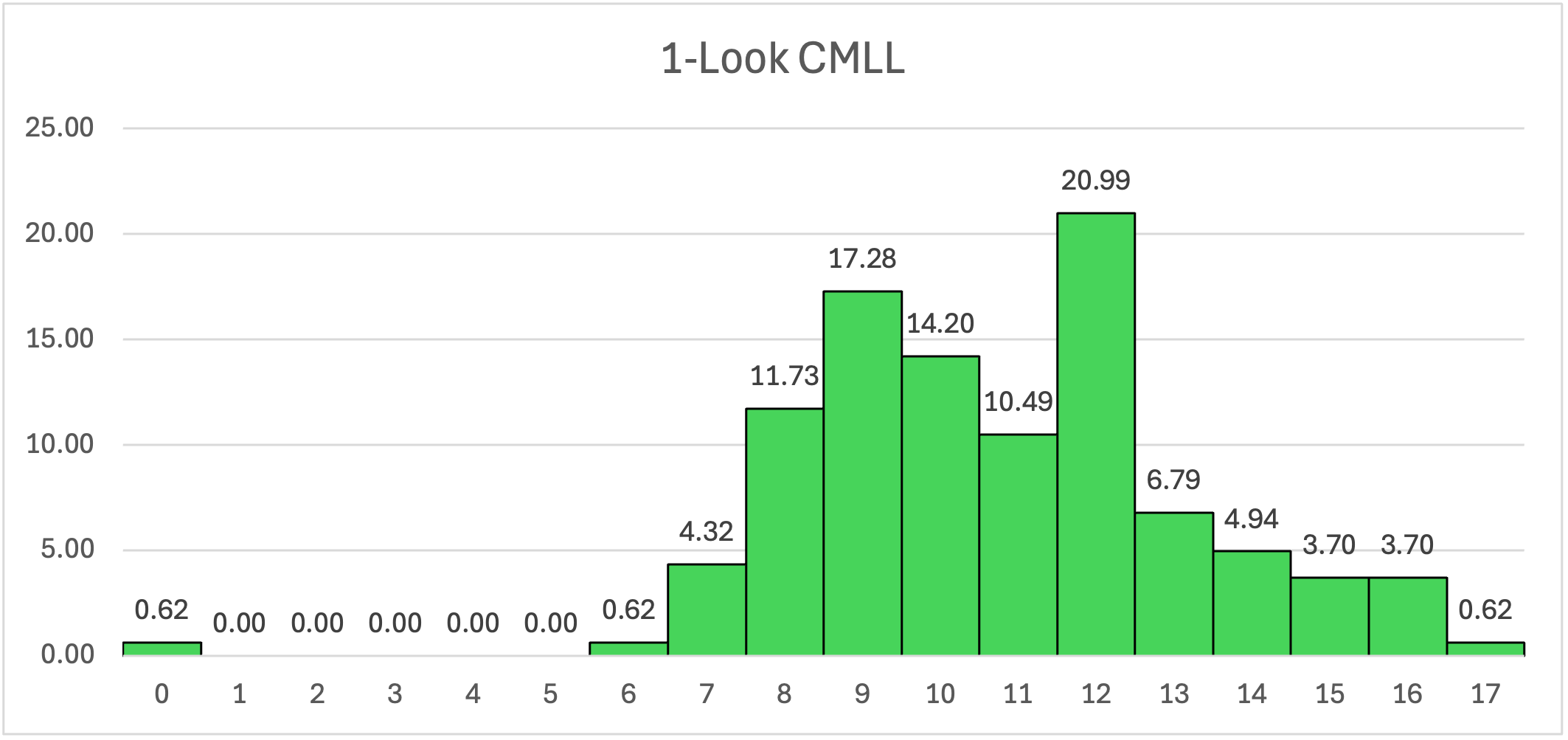
Novice 2-look CMLL is just a stepping stone to the real 1-look CMLL, because 2-look wastes a bunch of moves. Other CMLL schemes have been tried (liked permuting first then orienting) but they are consistently worse than just learning 1-look CMLL, which really isn't so hard. You know I have to make a graph for each step, so the exact comparison of 2-look and 1-look is below.
CMLL Statistics
| Average Moves | Standard Deviation | Median Moves | Max Moves | |
|---|---|---|---|---|
| 2-Look | 20.47 | 5.95 | 22 | 29 |
| 1-Look | 10.75 | 2.47 | 11 | 17 |
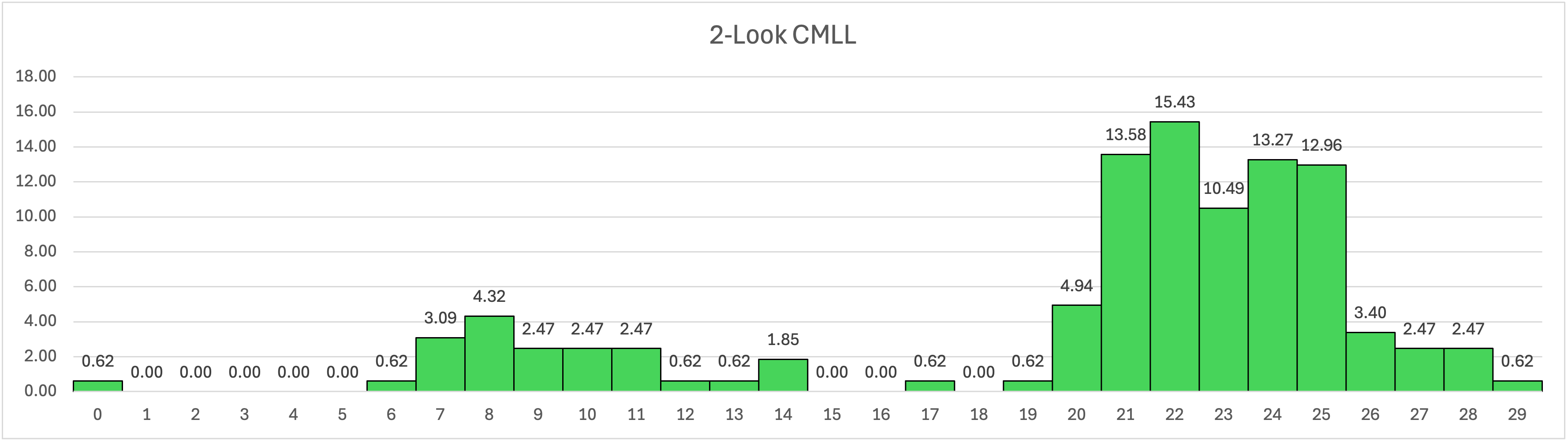
2-Look CMLL (Novice)
Orientation
2-Look CMLL starts by orienting all of the U-layer corners. There are 8 possible cases (including the case that they are oriented by default). Each of these cases has one or more common names vaguely based on how it looks as a picture, but most of the common names are approximately nonsense. All cube images on this page are viewed from above (looking down at the U face) with Blue defined to be the top color. Because we are only paying attention to orientation at first, right now we only care where the blue stickers are. Parentheses are included in some algorithms to help you visually organize the information. Once you have finished your first two blocks, making U turns only you can always make the top layer corner stickers take one of these 8 cases.
| Orientation skip! Move onto permutation for free! |
U or Headlights F (R U R' U') F' | ||
| Pi F (R U R' U') (R U R' U') F' (Just Headlights twice) |
H F (R U R' U') (R U R' U') (R U R' U') F' (Just Headlights thrice) |
||
| Sune R U R' U R U2 R' |
Antisune R' U' R U' R' U2 R | ||
| L or Bowtie F R U' R' U' R U R' F' |
T or Chameleon (R U R' U') (R' F R F') |
Permutation
Now all of your corners are oriented (Blue on top in our case). Next we have to permute them correctly. By turning the U layer you can bring the cube into one of 3 cases (including the solved case). The arrow shows what pieces need to be swapped. The stickers shown in pink squares determine the permutation case so you can do case recognition just by looking at those. |
Permutation skip! Move onto Last Six Edges for free! Recognition: two adjacent solved sides. |
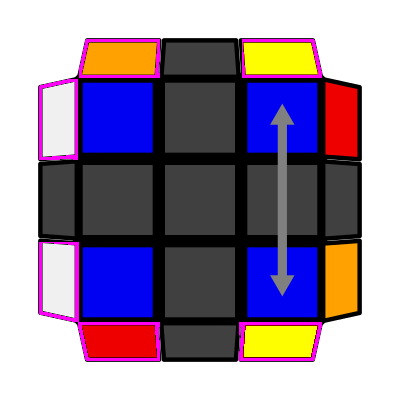 |
Adjacent swap Option 1: T-Perm = Chameleon then Bowtie R U R' U' R' F R2 U' R' U' R U R' F' Option 2: J-Perm (it's slightly better) R U R' F' R U R' U' R' F R2 U' R' Recognition: one solved side, adjacent to that you have two stickers which have adjacent colors to each other. |
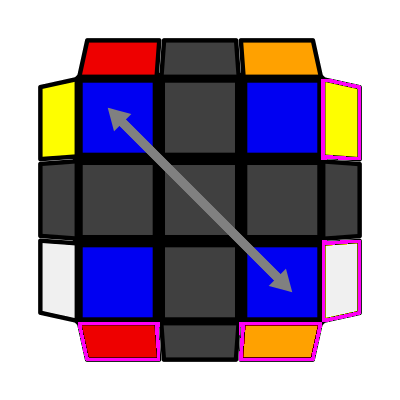 |
Diagonal swap Y-Perm = Bowtie then Chameleon F R U' R' U' R U R' F' (R U R' U') (R' F R F') Recognition: two adjacent sides where on each side the stickers are opposite colors to each other. |
1-Look CMLL (Intermediate & Advanced)
At Intermediate (I) and Advanced (A) levels, you perform both orientation and permutation of the top layer corners simultaneously. There are 43 cases (including the solved state). We break those 43 cases down into groups based on corner orientation. If the corners happen to be oriented by accident, you get one of the 3 permutation cases from 2-Look CMLL. There are 4 permutation cases for H orientation and 6 permutation cases for each of the other 6 orientations. (3 + 4 + 6x6 = 43)
The algorithms themselves for CMLL are nice and ergonomic. The hardest part isn't learning them, it is actually getting good at recognition which permutation state you are in. The location of the top color stickers on the four corners determines the orientation state. By also noting any one other sticker on each of the four corners, it determines the permutation state. Actually, even better, we only need one other sticker from three of the four corners to determine the permutation state. So, for each orientation state there are 4 standard stickers
to pay attention to. From any angle of looking at the cube you will always be able to see at least 3 of those standard stickers and so determine which CMLL case you have. At the intermediate level, you only have to learn 3 of the 4 standard stickers and so only learn how to recognize the case from one perspective (so at intermediate level you have to sometimes adjust the U layer before the algorithm to figure out what case you have). At the advanced level, you learn the fourth standard sticker so that you can recognize from any angle without unnecessary adjustment.
In the images below, I have labeled the standard stickers of each orientation by putting a pink square around them. There is always 1 standard sticker per corner. I number the standard stickers going clockwise around the U face. So, the standard sticker on the UBL corner is S1, on UBR is S2, on UFR is S3, and on UFL is S4. For each case, I write two recognition formulas (knowing both formulas covers all angles). Recognition formulas labeled with an I should be learned at intermediate level (and with an A learned at advanced level). For many cases there is actually a symmetry between the two formulas meaning learning one teaches you the other, so those ones you can actually recognize at any angle with just intermediate knowledge.
I put the orientation cases in the order I recommend learning them based on difficulty. I have also noted with the algorithms the probability (P: ) of getting each case overall in CMLL and the order (O: ) of the algorithm given (the order means how many times it has to be repeated to get back to where you started, as these are useful for practice). Algorithm orders are calculated only worrying about the 4 corners and ignoring any initial U move at the start of an algorithm.
Orientation Skip
The cases are just Permutation skip (P: 1/162, O: 0), adjacent swap (J-Perm, P: 2/81, O: 2), and diagonal swap (Y-Perm, P: 1/162, O: 2) from 2-Look CMLL with the same recognition scheme used there.
H
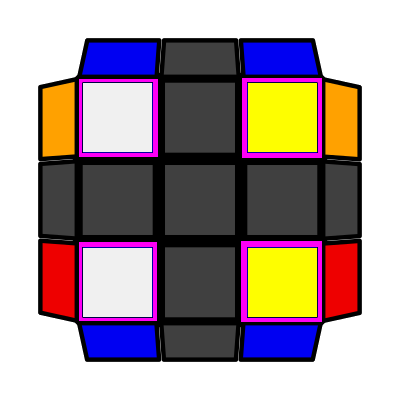 |
Columns (P: 1/81, O: 3) I: S1 = S4, S2 = S3 (R U2 R') U' (R U R' U') (R U' R') |
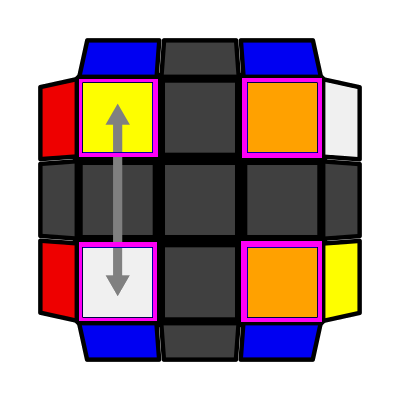 |
Single Column (P: 2/81, O: 4) I: S1 opp S4, S2 = S3 U F (R U' R' U) (R U2 R') U' (R U R' U') F' |
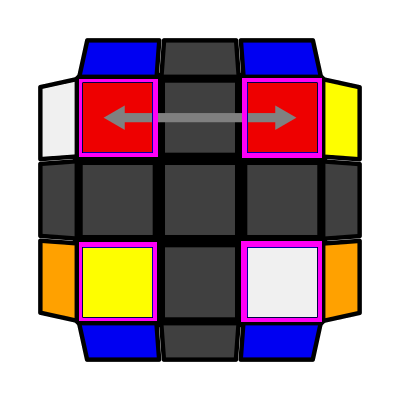 |
Single Row (P: 2/81, O: 4) I: S1 = S2, S3 opp S4 r U' r2 D' (r U' r') D r2 U r' |
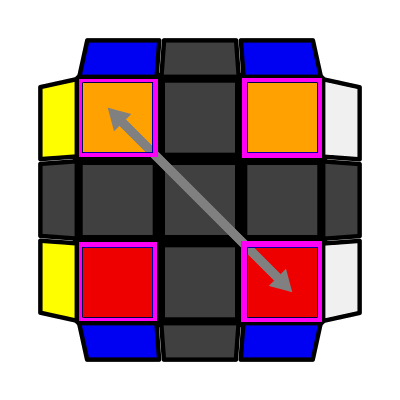 |
Rows (P: 1/81, O: 2) I: S1 = S2, S3 = S4 F (R U R' U') (R U R' U') (R U R' U') F' |
Pi
 |
Back Row (P: 2/81, O: 3) I: S1 = S2, S3 opp S4 U F (R U R' U') (R U R' U') F' |
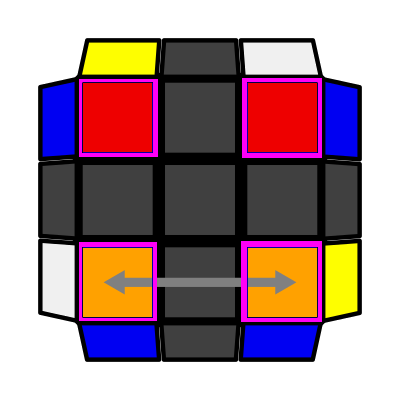 |
Rows (P: 2/81, O: 4) I: S1 = S2, S3 = S4 r U' r2 D' (r U r') D r2 U r' |
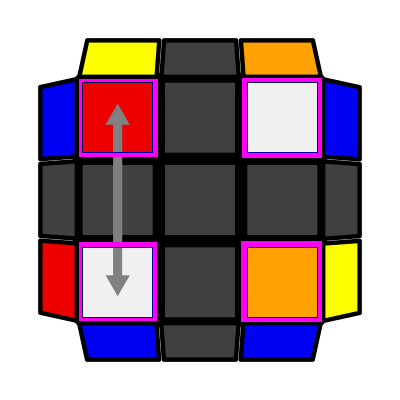 |
/ Up Slash (P: 2/81, O: 9) I: S1 opp S3, S2 = S4 U2 (F R' F' R) U2 (R U' R') U (R U2 R') |
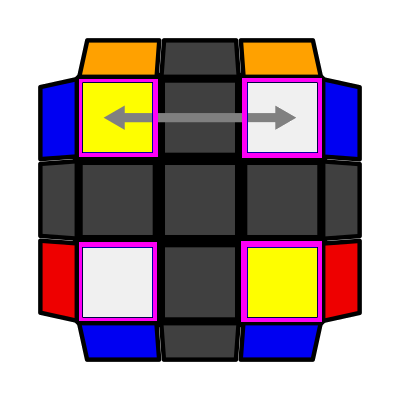 |
X Checkerboard (P: 2/81, O: 6)I: S1 = S3, S2 = S4 R' F R U F U' (R U R' U') F' |
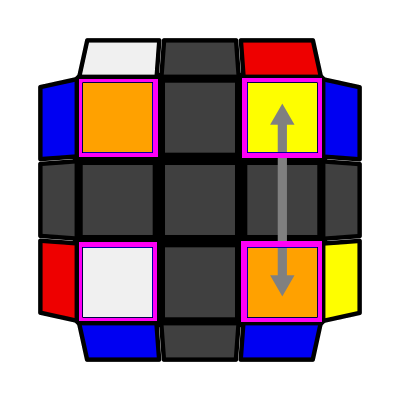 |
\ Down Slash (P: 2/81, O: 9) I: S1 = S3, S2 opp S4 U R U2 R' U' R U R' U2 R' F R F' |
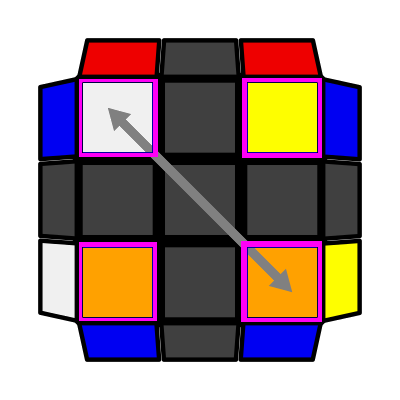 |
Front Row (P: 2/81, O: 6) I: S1 opp S2, S3 = S4 R' U' R' F R F' R U' R' U2 R |
Bowtie
 |
Adj Row (P: 2/81, O: 2) I: S1 = S2 adj S4 A: S2 opp S3 adj S4 U2 (R U2 R') U' (R U R' U') (R U R' U') (R U' R') |
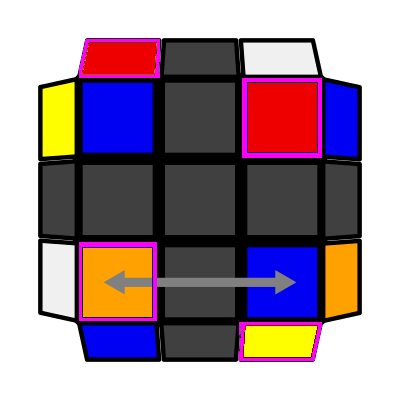 |
Opp Row (P: 2/81, O: 4) I: S1 = S2 opp S4 A: S2 opp S4 adj S3 F (R U' R') U' (R U R') F' |
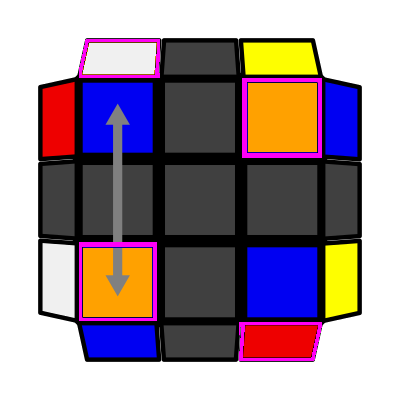 |
Opp / Slash (P: 2/81, O: 3) I: S4 = S2 opp S3 A: S4 = S2 adj S1 U' R' U2 R' D' (R U2 R') D R2 |
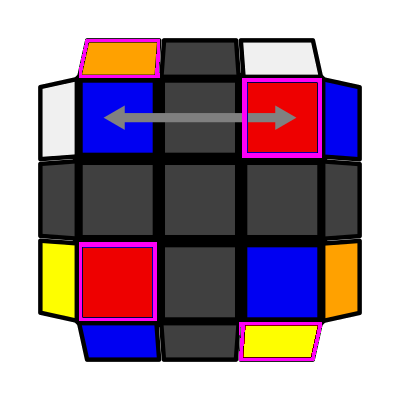 |
Adj / Slash (P: 2/81, O: 3)I: S4 = S2 adj S3 A: S4 = S2 opp S1 R U2 R D (R' U2 R) D' R2 |
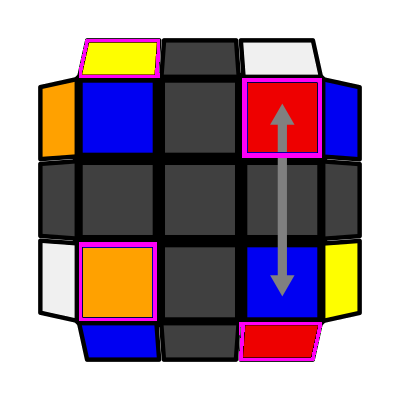 |
Opp Column (P: 2/81, O: 3) I: S2 = S3 opp S4 A: S2 opp S4 adj S1 (F R' F' R) (U R U' R') |
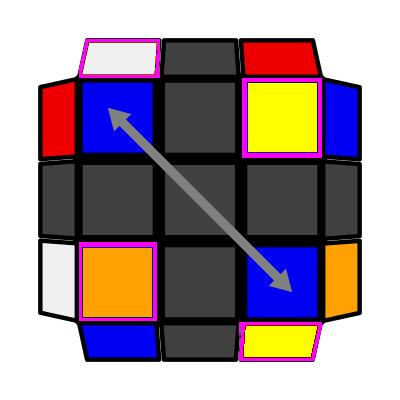 |
Adj Column (P: 2/81, O: 6) I: S2 = S3 adj S4 A: S1 opp S2 adj S4 R U2 R2 F R F' R U2 R' |
Headlights
 |
Columns (P: 2/81, O: 3) I: S2 = S3 opp S1 I (Symmetry): S1 = S4 opp S2 R2 F U' F U F2 R2 U' R' F R |
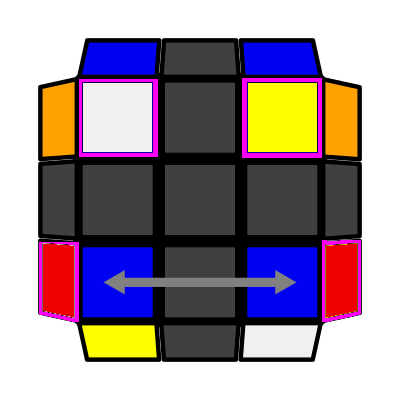 |
Front Row (P: 2/81, O: 4) I: S1 opp S2 adj S3 I (Sym): S1 opp S1 adj S4 U2 (r U' r') U r' D' (r U' r') D r |
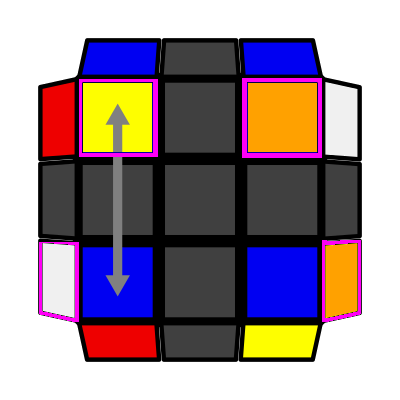 |
Right Column (P: 2/81, O: 3) I: S2 = S3 adj S1 A: S1 opp S2 adj S3R2 D' (R U2 R') D R U2 R |
 |
Back Row (P: 2/81, O: 9)I: S1 = S2 adj S3 I (Sym): S1 = S2 adj S4 U' F R2 D R' U R D' R2 U' F' |
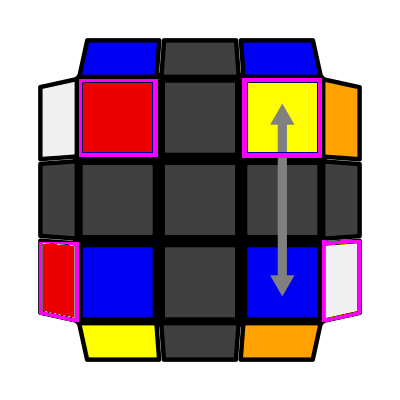 |
Left Column (P: 2/81, O: 3) I: S1 = S4 adj S2 A: S3 opp S2 adj S1 U2 R2 D (R' U2 R) D' R' U2 R' |
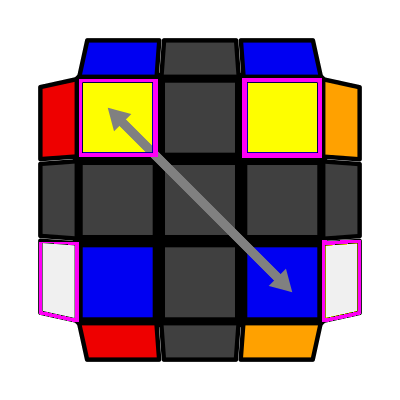 |
Rows (P: 2/81, O: 6) I: S1 = S2 opp S3 I (Sym): S1 = S2 opp S4 U' F (R U R' U') F' |
Chameleon
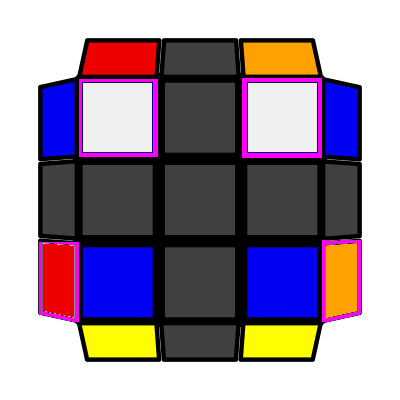 |
Back Row (P: 2/81, O: 4) I: S1 = S2 adj S3 I (Sym): S1 = S2 adj S4 F R' F R2 U' R' U' (R U R') F2 |
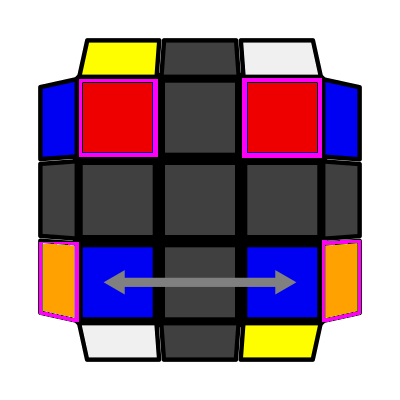 |
Rows (P: 2/81, O: 4) I: S1 = S2 opp S3 I (Sym): S1 = S2 opp S4 (r' D' r) U (r' D r) U' (r U r') |
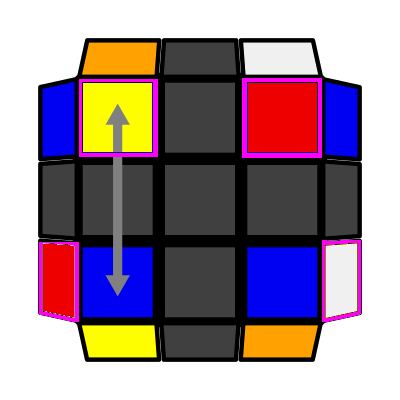 |
/ Up Slash (P: 2/81, O: 3) I: S2 = S4 adj S1 A: S1 opp S3 adj S2 U' (R U R' U') (R' F R F') |
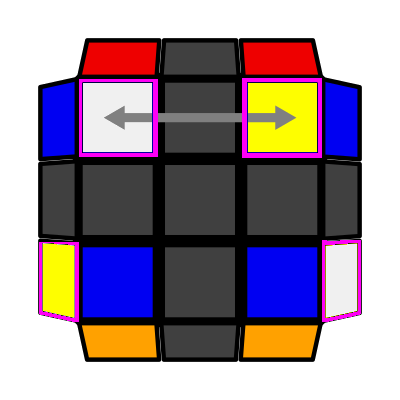 |
X Checkerboard (P: 2/81, O: 4)I: S1 = S3 opp S2 I (Sym): S2 = S4 opp S1 (r' U r) U2 R2 F R F' R |
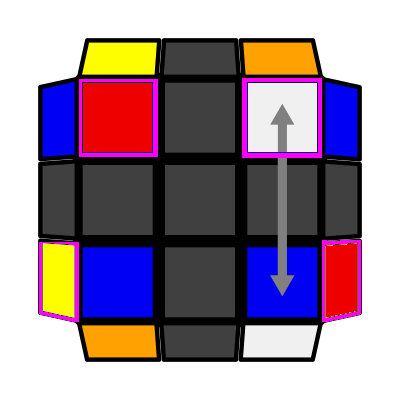 |
\ Down Slash (P: 2/81, O: 3) I: S1 = S3 adj S2 A: S2 opp S4 adj S1 U (L' U' L U) (L F' L' F) |
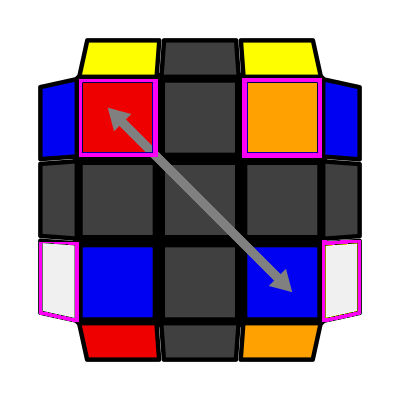 |
Front Row (P: 2/81, O: 6) I: S1 opp S2 adj S3 I (Sym): S1 opp S2 adj S4 U2 r2 D' (r U r') D r2 U' (r' U' r) |
Sune
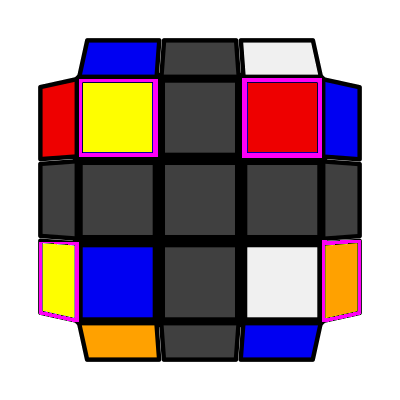 |
Left Column (P: 2/81, O: 6) I: S1 adj S2 opp S3 A: S1 = S4 adj S2 (R U R') U (R U2 R') |
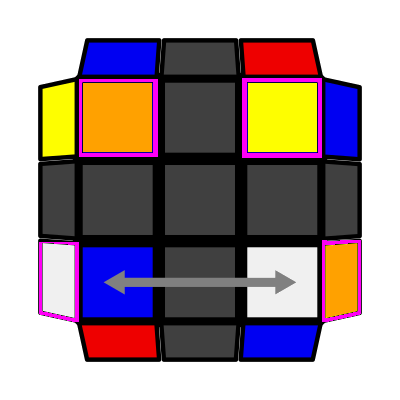 |
\ Down Slash (P: 2/81, O: 3)I: S1 = S3 adj S2 A: S2 opp S4 adj S1 (R U R' U') (R' F R F') (R U R') U (R U2 R') |
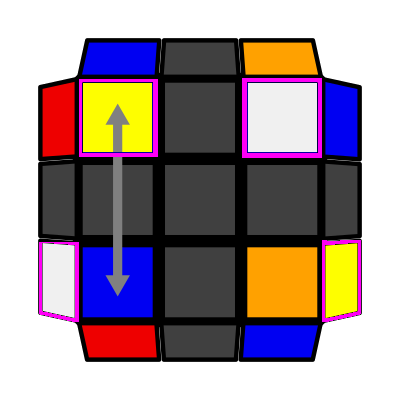 |
X Checkerboard (P: 2/81, O: 3) I: S1 = S3 opp S2 I (Sym): S2 = S4 opp S1 R U' L' U R' U' L |
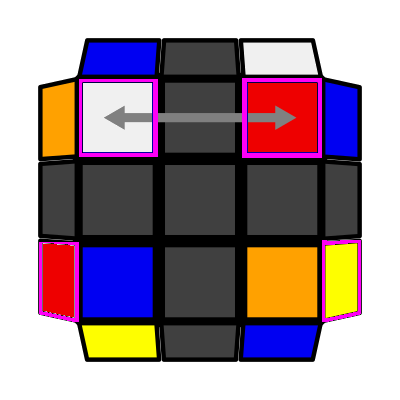 |
/ Up Slash (P: 2/81, O: 9)I: S1 opp S3 adj S2 A: S2 = S4 adj S1 (L' U2 L U2) (L F' L' F) |
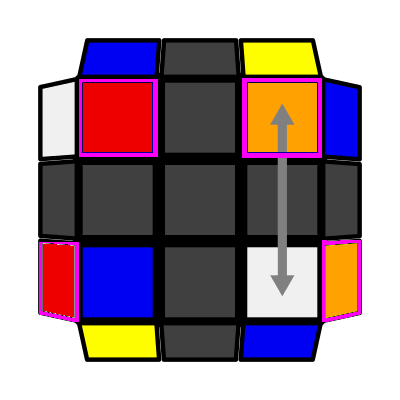 |
Columns (P: 2/81, O: 9) I: S1 opp S2 = S3 I (Sym): S2 opp S1 = S4 (F R' F' R) (U2 R U2 R') |
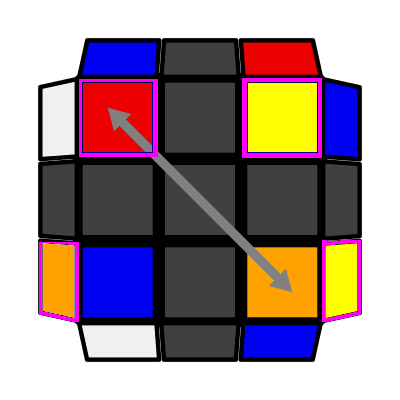 |
Right Column (P: 2/81, O: 6) I: S1 adj S2 = S3 A: S2 adj S1 opp S4 U2 (R U R') U (R' F R F') (R U2 R') |
Antisune
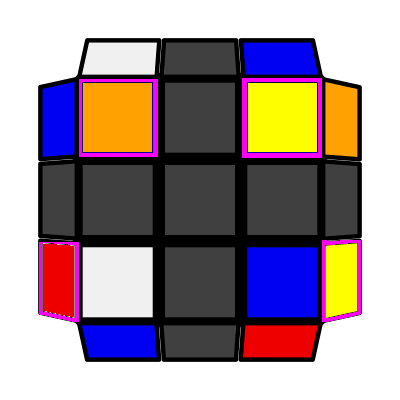 |
Right Column (P: 2/81, O: 6) I: S2 = S3 adj S1 A: S4 opp S1 adj S2 U2 (R' U' R) U' (R' U2 R) |
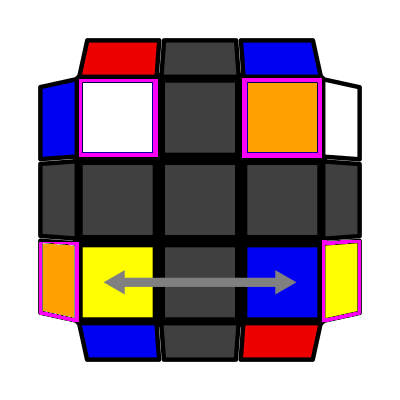 |
/ Up Slash (P: 2/81, O: 3) I: S1 opp S3 adj S2 A: S2 = S4 adj S1 R2 D (R' U R) D' R' U R' U' (R U' R') |
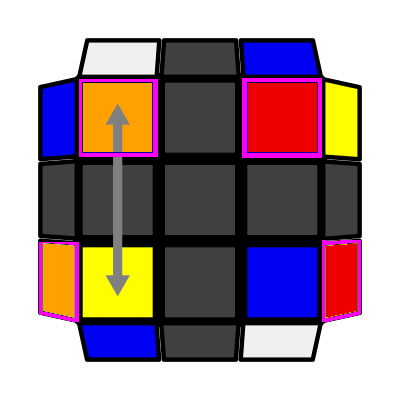 |
Columns (P: 2/81, O: 9) I: S1 opp S2 = S3 I (Sym): S2 opp S1 = S4 (F' L F L') (U2 L' U2 L) |
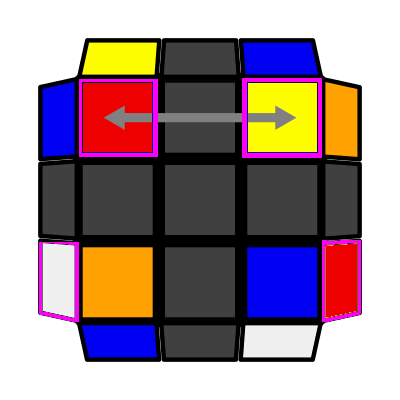 |
\ Down Slash (P: 2/81, O: 9)I: S1 = S3 adj S2 A: S1 adj S2 opp S4 (R U2 R' U2) (R' F R F') |
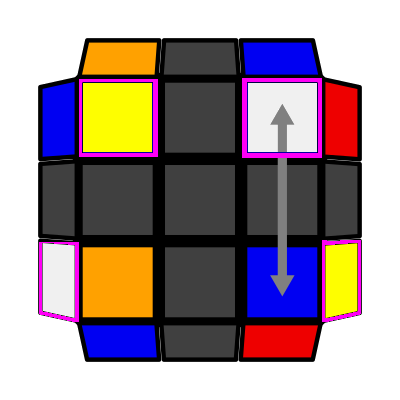 |
X Checkerboard (P: 2/81, O: 3) I: S1 = S3 opp S2 I (Sym): S2 = S4 opp S1 L' U R U' L U R' |
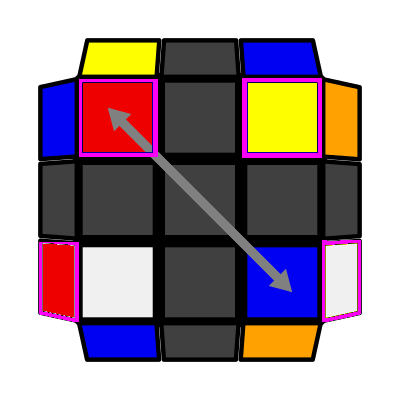 |
Left Column (P: 2/81, O: 6) I: S1 adj S2 opp S3 A: S4 = S1 adj S2 U (R' U' R) U' R' U (R' F R F') U R |